一类奇异二阶边值问题正解存在的充分必要条件

栾世霞, 赵艳玲

数学学报 ›› 2010, Vol. 53 ›› Issue (6) : 1163-1170.

PDF(421 KB)
中国科学院数学与系统科学研究院期刊网
PDF(421 KB)
数学学报 ›› 2010, Vol. 53 ›› Issue (6) : 1163-1170. DOI: 10.12386/A2010sxxb0129
论文

一类奇异二阶边值问题正解存在的充分必要条件

    栾世霞1, 赵艳玲1,2
作者信息 +

Necessary and Sufficient Condition for the Existence of Positive Solution to a Class of Singular Second-order Boundary Value Problems

    Shi Xia LUAN1, Yan Ling ZHAO1,2
Author information +
文章历史 +

摘要

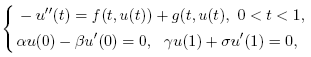本文利用锥拉伸与压缩不动点定理,在非线性项一个为超线性另一个有界及非线性项一个可以分解为超线性与次线性另一个有界的情况下,给出一类奇异二阶边值问题有一阶可导正解的充分必要条件,推广并改进了一些已知的结果.  

Abstract

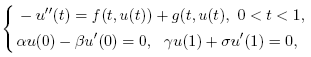In this paper, by using the tensile and the compression fixed-piont theorems in cone, a necessary and sufficient condition for the existence for the following nonlinear singular second-order boundry problem,,the is obtained under the condition that the nonlinear term is super-linear or sub-linear, or the nonlinear term is decomposed into super-linear and sub-linear, which imposed some known results.  

关键词

奇异二阶边值问题 / 正解 / 锥 / 超线性与次线性

Key words

second-oder singular boundary value problem / positive solutions / cone / necessary and sufficient condition

引用本文

EndNote

Ris (Procite)

Bibtex

导出引用
栾世霞, 赵艳玲. 一类奇异二阶边值问题正解存在的充分必要条件. 数学学报, 2010, 53(6): 1163-1170 https://doi.org/10.12386/A2010sxxb0129
Shi Xia LUAN, Yan Ling ZHAO. Necessary and Sufficient Condition for the Existence of Positive Solution to a Class of Singular Second-order Boundary Value Problems. Acta Mathematica Sinica, Chinese Series, 2010, 53(6): 1163-1170 https://doi.org/10.12386/A2010sxxb0129

参考文献



[1] Erbe L. H., Wang H. Y., On the existence of positive solutions of ordinary differential equations, Trans Amer. Math. Soc., 1994, 120(3): 143--748.



[2] Zhao Z. Q., Necessary and sufficient condition for the existence of positive solution to a class of singular sub-linear boundary value problems, Acta Mathematica Sinica, Chinese Series, 1998, 41(5): 1025--1034.



[3] Wei Z. L., Positive solutions of singular sublinear second order boundary value problems, Systems Science and Mathematical Science, 1998, 10(10): 82--88.



[4] Taliaferro S., In the positive solution of y'' + φ(t)(1/y) = 0, Nonlinear Analysis, 1978, 2: 437--446.



[5] Zhang Y., Positive solutions of singular Enden-Fowler boundary value problems, J. Math. Anal Appl., 1994, 185(1): 215--222.



[6] Pang C. C., Positive solutions of non-resonance super-linear singular Dirichlet boundary value problems, J. Sys. Sci. & Math. Sci., 2002, 22(1): 78--84.



[7] Hao Z. C., Mao A. M., Necessary and sufficient condition for the existence of positive solution to a class of singular second-order boundary value problems, J. Sys. Sci. & Math. Sci., 2001, 21(1): 93--100.



[8] Guo D. J., Lakshmikantham V., Nonlinear Problems in Abstact Cone, New York: Academic Press Inc, 1988.



[9] Mao A. M., Positive solutions of singular boundary value problems for super-linear positive exponent Enden-Fowler equation, Acta Mathematica Sinica, Chinese Series, 2000, 43(4): 623--632.



[10] Wei Z. L., Positive solutions of singular boundary value problems for super-linear Enden-Fowler equation, Acta Mathematica Scientia, 1998, 18: 115--118.



[11] Guo D. J., Nonlinear Functional Analysis, Ji'nan: Shandong Science and Technology Press, Second Edition, 2001, 8.



[12] Yang F. H., Necessary and sufficient condition for the existence of positive solution to a class of singular second-order boundary value problems, Chinese Journal of Engineering Mathematics, 2008 25(2): 281--287.



[13] Zhang X. G., Positive solutions of nonresonance semipositive singular Dirichlet boundary value problems, Nonlinear Analysis, 2008, 68: 97--108.

基金

国家自然科学基金(10771117);山东省青年基金(Q2007A02)和自然科学基金(ZR2009AL016)资助

PDF(421 KB)

254

Accesses

0

Citation

Detail
段落导航
相关文章

/

〈 〉